2.Data Exploration

1.What is data exploration?

• A preliminary exploration of the data to better understand its characteristics.
  • Key motivations of data exploration include
    • Helping to select the right tool for preprocessing or analysis
    • Making use of humans’ abilities to recognize patterns
      • People can recognize patterns not captured by data analysis tools
  • Related to the area of Exploratory Data Analysis (EDA)
    • Created by statistician John Tukey
    • Seminal book is Exploratory Data Analysis by Tukey
    • A nice online introduction can be found in Chapter 1 of the NIST/SEMATECH e-Handbook of Statistical Methods http://www.itl.nist.gov/div898/handbook/index.htm

• Techniques Used In Data Exploration

  • In EDA, as originally defined by Tukey
    • The focus was on visualization
    • Clustering and anomaly detection were viewed as exploratory techniques
    • In data mining, clustering and anomaly detection are major areas of interest, and not thought of as just exploratory
  • In our discussion of data exploration, we focus on
    • Summary statistics
    • Visualization
    • Online Analytical Processing (OLAP)
• Iris Sample Data Set
  • Many of the exploratory data techniques are illustrated with the Iris Plant data set.
  • Can be obtained from the UCI Machine Learning Repository 
http://www.ics.uci.edu/~mlearn/MLRepository.html
  • From the statistician Douglas Fisher
  • Three flower types (classes):
    • Setosa
    • Virginica
    • Versicolour
  • Four (non-class) attributes
    • Sepal width and length
    • Petal width and length

2.Summary Statistics

• Summary statistics are numbers that summarize properties of the data

  • Summarized properties include frequency, location and spread
    • Examples: location - mean
 spread - standard deviation
  • Most summary statistics can be calculated in a single pass through the data
• Frequency and Mode
  • The frequency of an attribute value is the percentage of time the value occurs in the data set
    • For example, given the attribute ‘gender’ and a representative population of people, the gender ‘female’ occurs about 50% of the time.
  • The mode of an attribute is the most frequent attribute value
  • The notions of frequency and mode are typically used with categorical data
• Percentiles

  • For continuous data, the notion of a percentile is more useful.

  • Given an ordinal or continuous attribute x and a number p between 0 and 100, the pth percentile is a value xp of x such that p% of the observed values of x are less than xp.

  • For instance, the 50th percentile is the value x50% such that 50% of all values of x are less than x50%.

• Measures of Location: Mean and Median

  • The mean is the most common measure of the location of a set of points.
  • However, the mean is very sensitive to outliers.
  • Thus, the median or a trimmed mean is also commonly used.

• Measures of Spread: Range and Variance

  • Range is the difference between the max and min
  • The variance or standard deviation sx is the most common measure of the spread of a set of points.
  • Because of outliers, other measures are often used.

3.Visualization

• 3.1 Representation

  • Visualization is the conversion of data into a visual or tabular format so that the characteristics of the data and the relationships among data items or attributes can be analyzed or reported.

  • Visualization of data is one of the most powerful and appealing techniques for data exploration.

    • Humans have a well developed ability to analyze large amounts of information that is presented visually

    • Can detect general patterns and trends

    • Can detect outliers and unusual patterns

  • Is the mapping of information to a visual format

  • Data objects, their attributes, and the relationships among data objects are translated into graphical elements such as points, lines, shapes, and colors.

  • Example:

    • Objects are often represented as points
    • Their attribute values can be represented as the position of the points or the characteristics of the points, e.g., color, size, and shape
    • If position is used, then the relationships of points, i.e., whether they form groups or a point is an outlier, is easily perceived.

• 3.2 Arrangement

  • Is the placement of visual elements within a display
  • Can make a large difference in how easy it is to understand the data

Problem with large number of partitions

• Node impurity measures tend to prefer splits that result in large number of partitions, each being small but pure

  • Customer ID has highest information gain because entropy for all the children is zero

Gain Ratio: - Adjusts Information Gain by the entropy of the partitioning (). - Higher entropy partitioning (large number of small partitions) is penalized! - Used in C4.5 algorithm - Designed to overcome the disadvantage of Information Gain

• 3.3 Selection

  • Is the elimination or the de-emphasis of certain objects and attributes
  • Selection may involve the choosing a subset of attributes
    • Dimensionality reduction is often used to reduce the number of dimensions to two or three
    • Alternatively, pairs of attributes can be considered
  • Selection may also involve choosing a subset of objects
    • A region of the screen can only show so many points
    • Can sample, but want to preserve points in sparse areas

3.3.3 Measure of Impurity: Classification Error

• Classification error at a node 

  • Maximum of when records are equally distributed among all classes, implying the least interesting situation
  • Minimum of 0 when all records belong to one class, implying the most interesting situation

Misclassification Error vs Gini Index

• 3.4 Techniques

  • Histograms

    • Usually shows the distribution of values of a single variable
    • Divide the values into bins and show a bar plot of the number of objects in each bin.
    • The height of each bar indicates the number of objects
    • Shape of histogram depends on the number of bins
  • Two-Dimensional Histograms
    • Show the joint distribution of the values of two attributes

  • Box Plots, Scatter Plots, Contour Plots, Matrix Plots

    • Box Plots
      • Invented by J. Tukey
      • Another way of displaying the distribution of data
      • Following figure shows the basic part of a box plot

    

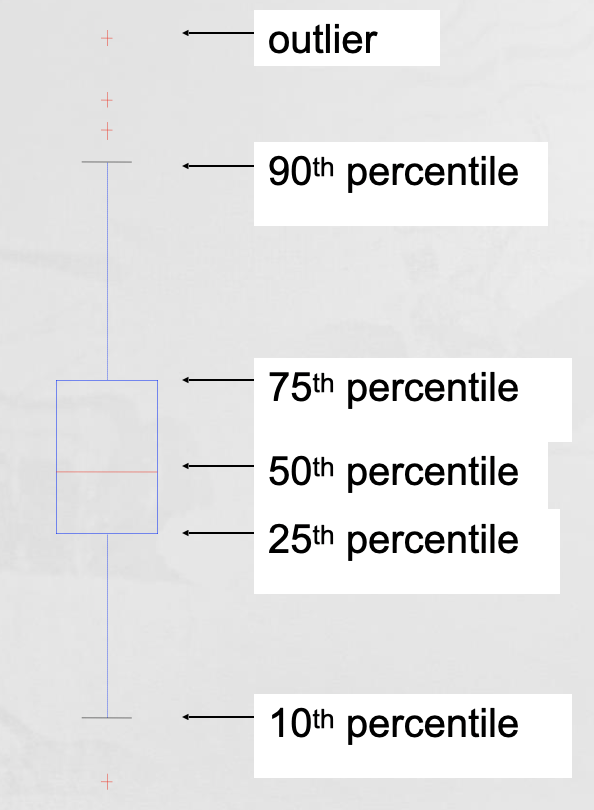
    • Scatter plots
      • Attributes values determine the position
      • Two-dimensional scatter plots most common, but can have three-dimensional scatter plots
      • Often additional attributes can be displayed by using the size, shape, and color of the markers that represent the objects
      • It is useful to have arrays of scatter plots can compactly summarize the relationships of several pairs of attributes
    • Contour plots
      • Useful when a continuous attribute is measured on a spatial grid
      • They partition the plane into regions of similar values
      • The contour lines that form the boundaries of these regions connect points with equal values
      • The most common example is contour maps of elevation
      • Can also display temperature, rainfall, air pressure, etc.
    • Matrix plots
      • Can plot the data matrix
      • This can be useful when objects are sorted according to class
      • Typically, the attributes are normalized to prevent one attribute from dominating the plot
      • Plots of similarity or distance matrices can also be useful for visualizing the relationships between objects

  • Parallel Coordinates

    • Parallel Coordinates
      • Used to plot the attribute values of high-dimensional data
      • Instead of using perpendicular axes, use a set of parallel axes
      • The attribute values of each object are plotted as a point on each corresponding coordinate axis and the points are connected by a line
      • Thus, each object is represented as a line
      • Often, the lines representing a distinct class of objects group together, at least for some attributes
      • Ordering of attributes is important in seeing such groupings
    • Star Plots
      • Similar approach to parallel coordinates, but axes radiate from a central point
      • The line connecting the values of an object is a polygon
    • Chernoff Faces
      • Approach created by Herman Chernoff
      • This approach associates each attribute with a characteristic of a face
      • The values of each attribute determine the appearance of the corresponding facial characteristic
      • Each object becomes a separate face
      • Relies on human’s ability to distinguish faces

  • Star Plots, Chernoff faces

    • On-Line Analytical Processing (OLAP) was proposed by E. F. Codd, the father of the relational database.
    • Relational databases put data into tables, while OLAP uses a multidimensional array representation.
    • Such representations of data previously existed in statistics and other fields
    • There are a number of data analysis and data exploration operations that are easier with such a data representation.